Глава 5.Составление уравнений САР. Устойчивость САР

5.1.Составление уравнений САР

Уравнение системы составляется с использованием как аналитических характеристик отдельных звеньев, так и экспериментальных. Составление уравнения сводится к следующим этапам:

- составление функциональной схемы САР;
- составление структурной схемы САР;
-определение динамических характеристик отдельных звеньев, например, способом опознавания W(p) элемента и определение его параметров по экспериментальным характеристикам;
- упрощение характеристик реальных звеньев путем их линеаризации и понижения порядка уравнений;
- преобразование структурной схемы в одноконтурную;
- вычисление W(p) САР в разомкнутом виде;
-составление уравнения замкнутой САР с учетом внешних возмущений.

Если рассматривать простейшую одноконтурную САР, состоящую из n звеньев (рис.21), соединенных

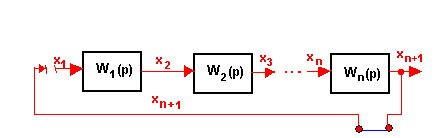
Рис.21 – Простейшая одноконтурная САР

последовательно, в разомкнутом виде, т.е. при разрыве одной из связей, то передаточная функция разомкнутой САР будет иметь вид:

W(p)=W₁(p)·W₂ (p)·...·W_n (p)=x_n+1(p)/x₁ (p).

Передаточную функцию можно представить в виде отношения коэффициента передачи K(p)=K₁(p)· ·K₂(p)·...·K_n(p)

к характеристическому оператору H(p)=H₁(p)·H₂(p)·...·H_n(p), где К(р) и Н(р) - операторы соответственно правой и левой частей дифференциальных уравнений звеньев или всей системы в целом. Замкнув систему, можно определить ее передаточную функцию в замкнутом состоянии W_з(p), с учетом того, что САР представляет собой систему с отрицательной обратной связью, передаточная функция которой W_ос(p)=1:

W_з(p)= W(p)/[1+ W(p)].

Это уравнение определяет связь между передаточными функциями W(p) разомкнутой и замкнутой W_з(p) системами.

В любой САР имеется два типа воздействий: управляющие, которые система должна воспроизводить, и возмущающие, которые она должна подавлять. Рассмотрим простейшую САР, состоящую из объекта регулирования с передаточной функцией W_об(p) и регулятора с передаточной функцией W_р(p) (рис.22), с одним возмущающим воздействием f(p), приложенным к входу объекта. Передаточная функция САР будет иметь следующий вид:

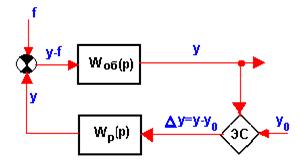
Рис.22 – К расчету уравнения САР

а) ошибка относительно внешнего возмущения

Wf(p)=Δy(p)/f(p)=W_o(p)/[1+ W_o(p)·W_p(p)];

б) ошибка относительно возмущения по заданию

Wу₀(p)= Δy(p)/σ₀(р)=1/[1+ W_o(p)·W_p(p)].

Следовательно, передаточная функция замкнутой САР зависит от вида возмущения и от точки его приложения. В общем случае для одноконтурной линейной САР

W_з(p)=Wfy(p)/[1+ W(p)],

где W(p) и Wfy(p) -передаточные функции всей системы в разомкнутом состоянии и цепи передачи воздействия между точками приложения возмущения f(р) и съемом выходной величины у. Уравнение замкнутой системы можно получить, приравнивая к нулю произведение операторного многочлена на координату системы:

[H(p)+K(p)]·y(p)=0.

Если система является невозмущенной, то уравнение не зависит от того, относительно какой координаты оно составлено. При наличии внешнего возмущения f(р) уравнение записывается в виде

[H(p)+K(p)]·y(p)= f(р),

где y(p) - выходная координата системы ( в САР обычно отклонение регулируемой величины);

f(р) - возмущение, пересчитанное на точку приложения.

Введем понятие о характеристическом уравнении системы. Для разомкнутой САР это уравнение получается приравниванием нулю знаменателя передаточной функции H(p)=0, для замкнутой

W_з(p)= W(p)/[1+ W(p)]= K(p)/[H(p)+K(p)]

и характеристическое уравнение имеет вид) [H(p)+K(p)]=0, т.е. характеристическое уравнение получается путем приравнивания нулю суммы операторов правой и левой частей дифференциального уравнения системы.

5.2.Качественные критерии устойчивости САР

Устойчивость САР -это способность ее возвращаться в состояние равновесия после прекращения возмущения. Устойчивость -это главное свойство САР. Только к устойчивой САР можно предъявлять различные требования. При нарушении равновесия внешними возмущениями возникает переходной процесс. Об устойчивости САР можно судить по характеру реакции ее на внешнее возмущение, например, на единичное скачкообразное возмущение. Затухающий переходной процесс (рис.23,а) свидетельствует об устойчивости САР, расходящийся (рис.23,б) - об ее неустойчивости.

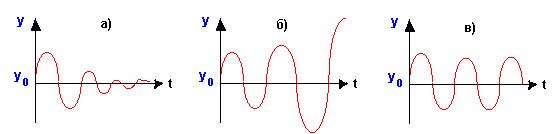
Рис.23 – Кривые переходных процессов

Переходной процесс в виде незатухающих колебаний с постоянной амплитудой (рис.23,в) характеризует линейную САР, находящуюся на грани устойчивости (неустойчивости). Вопрос о работоспособности САР с колебательными переходными процессами решается в зависимости от конкретных условий. Если колебания регулируемой величины не выходят за пределы допустимых отклонений, а периодические изменения режима объекта, соответствующие воздействию регулятора на объект, не снижают надежности работы оборудования, то такие САР могут считаться устойчивыми или работоспособными.

Об устойчивости линейной САР можно судить также по корням ее характеристического уравнения, полученного заменой в ее дифференциальном уравнении производных оператором р со степенями, соответствующими порядку производных:

a_npⁿ + a_n-1p^n-1+…+a₁p +a₀=0.

Характеристическое уравнение астатической системы отличается от приведенного отсутствием свободного члена а₀. В общем случае корни характеристического уравнения, как правило, комплексные, попарно сопряженные, вида

p_i =α_i ±jβ_i.

Необходимым и достаточным условием устойчивости САР является отрицательные значения вещественных частей всех корней характеристического уравнения. Наличие хотя бы одного корня (комплексного или вещественного) с положительной вещественной частью свидетельствует об неустойчивости САР. САР, имеющая чисто мнимые корни, находится на грани устойчивости. Корни характеристического уравнения можно представить в виде точек на плоскости корней, т.е. комплексной плоскости, образованной вещественной осью α и мнимой β. Линейная САР устойчива, если все корни характеристического уравнения располагаются на комплексной плоскости корней слева от

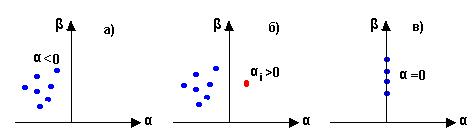
Рис.24 – К вопросу устойчивости САР

мнимой оси (рис.24,а); если хотя бы один корень располагается справа от мнимой оси (рис.24,б) САР неустойчива; если все корни располагаются на мнимой оси (рис.24,в) САР находится на грани устойчивости. При использовании рассмотренного условия устойчивости САР, описываемых уравнениями выше четвертого порядка, возникают затруднения в вычислении корней. Поэтому разработаны критерии устойчивости системы автоматического регулирования без необходимости вычисления корней характеристического уравнения. Различают критерии двух категорий: алгебраические и частотные. К первым относится критерий Рауса-Гурвица, ко вторым -критерии Михайлова и Найквиста. Алгебраические критерии основаны на исследовании коэффициентов линейного дифференциального уравнения САР, а именно, удовлетворяют ли эти коэффициенты определенным требованиям. В соответствии с критерием Рауса-Гурвица САР устойчива, если все определители Гурвица ∆_к и коэффициенты дифференциального уравнения а_n положительны, иначе -САР не устойчива. Применение критерия Гурвица как и других алгебраических критериев связано со следующими недостатками.

1.Требуются вычисления, трудность которых возрастает с увеличением порядка уравнения САР. 2.Алгебраические критерии применять нельзя, если известны не уравнения системы, а экспериментальные характеристики САР или отдельных ее звеньев.
3.Коэффициенты уравнения фигурируют в этих критериях в столь сложных сочетаниях, что трудно выявить влияние отдельных коэффициентов (т.е. характеристик отдельных звеньев) на устойчивость САР.

5.3.Частотные критерии устойчивости САР

Критерии устойчивости, основанные на исследовании частотных характеристик, свободны от перечисленных недостатков алгебраических критериев. Они дают геометрическую интерпретацию устойчивости, обладают большой наглядностью, позволяют использовать экспериментальные характеристики звеньев и дают возможность определить влияние параметров отдельных звеньев на устойчивость системы в целом. Наибольшее применение имеют критерии Михайлова и амплитудно-фазочастотный критерий Найквиста.

Критерий Найквиста основан на исследовании расположения АФЧХ САР на комплексной плоскости. Достоинством этого критерия является то, что он позволяет судить об устойчивости САР по АФЧХ разомкнутой системы, которую проще определить, чем для замкнутой. Согласно этому критерию, САР устойчивая в разомкнутом состоянии, устойчива и в замкнутом, если годограф АФЧХ разомкнутой системы (при изменении частоты ω от 0 до +∞) не охватывает точки комплексной плоскости с координатами (-1; j0), лежащей на отрицательной вещественной полуоси. Если годограф АФЧХ не охватывает точку с координатами (-1; j0) САР устойчива - кривые 1 на рис.25,а,б; если точка с координатами (-1; j0) лежит в плоскости годографа -САР не устойчива (кривые 3 на рис.25,а,б); если годограф

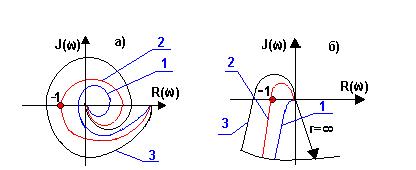
Рис.25 –Годографы АФЧХ САР: а-статических; б-астатических

проходит через точку (-1; j0) -САР находится на грани устойчивости (кривые 2 на рис.25,а,б,). Говоря, что годограф W(jω) не охватывает точки (-1; j0), подразумевают, что эта точка находится вне контура, образованного годографом при изменении частоты ω=0 и ω=+∞ (рис.25,а), для астатических САР годограф при этом условно дополняется дугой бесконечно большого радиуса (рис.25,б).

Критерий Найквиста позволяет определить запас устойчивости системы, т.е. величину возможных изменений ее параметров, не приводящих к потере устойчивости. Запас устойчивости определяется раздельно по модулю и фазе W(jω). Наиболее распространенным является определение запасов устойчивости по положению годографа W(jω) относительно окружности единичного радиуса с центром в начале координат (рис.26) Запас устойчивости по модулю:

З_м=AB/OA,

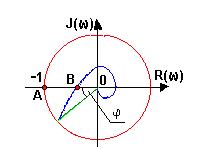
Рис.26 – К определению запаса устойчивости САР

(в долях единицы или процентах), т.е. равен отношению длины отрезка вещественной оси, заключенного между точкой (-1; j0) и точкой пересечения годографа с вещественной отрицательной полуосью к отрезку длиной равной единице. Запас устойчивости по фазе равен углу φ, образованному отрицательной вещественной полуосью и прямой, проведенной из начала координат в точку пересечения годографа с окружностью единичного радиуса.

Для качественной работы САР недостаточна одна ее устойчивость, необходимы и другие качества. Наиболее распространенными являются количественные оценки динамических качеств САР, полученные по ее переходным характеристикам (кривым регулирования, построенным аналитически или в результате эксперимента), так называемые прямые оценки качества регулирования. К ним относятся статическая точность САР, динамическая точность САР, перерегулирование, быстродействие, колебательность процесса и др.

Контрольные вопросы

1.Укажите основные этапы при составлении уравнений САР.
2.Что такое характеристическое уравнение системы?
3.Что понимается под устойчивостью САР?
4.Какие Вы знаете критерии устойчивости САР?
5.Укажите основные преимущества критерия устойчивости Найквиста.
6.Как определяется запас устойчивости САР?

Вернуться к началу главы

Вернуться к началу учебника