Глава 4. Динамические свойства САР

4.1. Дифференциальные уравнения и передаточные функции САР

Динамические свойства системы можно описать аналитическими или экспериментальными характеристиками. К первым относятся дифференциальные уравнения и передаточные функции. Дифференциальные уравнения

а_n·(dⁿ y/dtⁿ) + a_n-1·(d^n-1y/dt^n-1) + …+a₁·(dy/dt) + a₀·y =

=b_m·(d^m x/dt^m) + b_m-1·(d^m-1x/dt^m-1) + …+b₁·(dx/dt) + b₀·y,

где а и b – постоянные коэффициенты;

m≤n – целые числа.

Постоянные коэффициенты характеризуют параметры системы.

П е р е д а т о ч н а я функция W(p) – это отношение преобразования Лапласа для выходной величины к преобразованию Лапласа для входной величины при нулевых начальных условиях. Формально W(p) представляет собой более удобный вид записи дифференциального уравнения с заменой операции дифференцирования умножением на оператор р=(d/dt).

Преобразования Лапласа позволяет заменить функцию вещественного переменного, например, времени f(t), функцией комплексного переменного F(p) при помощи интеграла

В преобразовании Лапласа функция вещественного переменного f(t) называется оригиналом, функция комплексного переменного F(p) называется изображением. Переход от оригинала f(t) к изображению F(p) записывается в виде прямого преобразования Лапласа

F(p)=L[f(t)],

переход от изображения к оригиналу записывается в виде обратного преобразования Лапласа

f(t)=L^-1[F(p)].

Каждой операции над оригиналом соответствует определенная операция над изображением. В частности, операциям дифференцирования и интегрирования оригиналов соответствуют более простые операции умножения и деления изображений на оператор р в степени, соответствующей порядку производной или кратности интеграла.

Обозначив преобразование Лапласа для х(t) через x(p) и для y(t) через y(p) т.е. x(p)=L[x(t)] , y(p)=L[y(t)]. Применив преобразование Лапласа к дифференциальному уравнению системы при нулевых начальных условиях, получим уравнение САР в операторной форме

y(p) ·[a_npⁿ + a_n-1p^n-1+…+a₁p +a₀]=x(p) ·[b_mp^m+b_m-1p^m-1+…+b₁p+b₀].

C уравнением в операторной форме можно выполнять любые действия как с обыкновенным алгебраическим уравнением, и, в частности, вычислить

W(p) = y(p)/ x(p) = [b_mp^m+b_m-1p^m-1+…+b₁p+b₀] / [a_npⁿ + a_n-1p^n-1+…+a₁p +a₀]=K(p) / H(p),

Таким образом, передаточная функция вычисляется из дифференциального уравнения как частное от деления оператора К(р) его правой части на оператор H(p) левой части. При р=0, в установившемся режиме, W(0) =b₀/a₀ =K – передаточная функция становится равной статическому коэффициенту передачи. Для линейных систем передаточная функция (как и диф. уравнение) исчерпывающе характеризует реакцию системы на любые возмущения, так как W(p) не зависит от формы возмущения. Зная W(p), можно определить y(p) и y(t):

y(p)= x(p)· W(p) ; y(t)= L^-1[x(p)· W(p)],

( т.е. чтобы определить реакцию системы y(t), необходимо найти изображение возмущения x(p), умножить его на передаточную функцию, а затем перейти от изображения к оригиналу. Пользуясь этим правилом, можно установить, как проходит через линейную систему сигнал любой формы.

4.2.Экспериментальные динамические характеристики САР

В ряде случаев динамические свойства достаточно полно могут быть описаны экспериментальными характеристиками. Экспериментальные динамические характеристики показывают, как реагирует система на типовые стандартные возмущения -ступенчатое, импульсное, гармоническое. Рассмотрим динамические характеристики, имеющие наибольшее практическое значение.

Переходная характеристика h(t) - (рис.16) описывает реакцию системы на типовое ступенчатое однократное

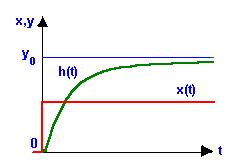
Рис.16 – Переходная характеристика САР

скачкообразное возмущение, т.е. переходной процесс, вызванный этим возмущением. Для t<0 x(t)=0; t ≥ 0 x(t)=const. Обычно рассматривается единичное ступенчатое возмущение u(t)=x(t)=1 при t ≥0. Это возмущени является наиболее распространенным на практике (мгновенный сброс или приложение нагрузки, скачок температуры, давления, напряжении т.п.). По виду h(t) можно определить общие динамические свойства системы. Аналитическое уравнение переходной функции h(t) можно получить, решая диф. уравнение системы при x(t)=1(t) и нулевых начальных условиях. Связь между h(t) и W(p) устанавливается следующим образом. Изображение по Лапласу единичной функции L[u(t)]=1/p соответствует изображение выходной величины

y(p)=(1/p)∙ W(p).

Переходя от изображения к оригиналу получим

y(t)= h(t)= L^-1[ W(p)/p],

т.е. для нахождения переходной функции необходимо умножить передаточную функцию на 1/p, а затем найти оригинал этого изображения.

Частотные характеристики (ЧХ) описывают реакцию системы в установившемся состоянии на входное возмущение, представляющее собой периодическую функцию времени, т.е. линейную комбинацию sin ωt, cos ωt, где ω=2πf -круговая частота.

Рис.17 – Типы возмущений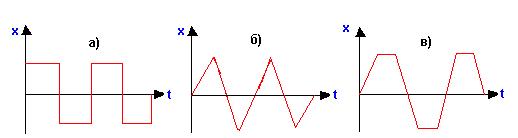

На практике необходимо знать реакцию системы на наиболее часто встречающиеся возмущения типа прямоугольная (рис.17,а), треугольная (рис.17,б), трапецеидальная (рис.17,в) волна и др. Получить аналитическое описание таких возмущений довольно сложная задача. Поэтому такие возмущения разлагаются в ряды Фурье и реакция САР исследуется на гармонические составляющие этого разложения.

Рассмотрим основные виды частотных характеристик и их физический смысл. Если на вход линейной САР подать гармонические возмущения вида x(t)=X·sin(ωt), или в показательной форме записи комплексного числа

X' =X·e^jωt ,

то после завершения переходного процесса на выходе установятся гармонические колебания (рис.18),

y(t)=Y· sin(ωt+φ)

или в показательной форме записи комплексного числа

Y' =Y· e ^j(ωt+φ).

Рис.18 – Переходной процесс в САР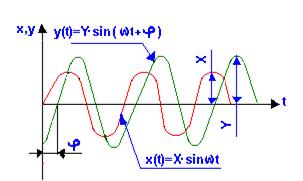

Частота колебаний на входе и выходе совпадают, но их амплитуды и фазы в общем случае отличаются. Если при постоянных амплитуде и фазе входных колебаний изменять их частоту и при этом измерять амплитуды и фазы выходных установившихся колебаний, то можно определить следующие общепринятые частотные характеристики:

1)амплитудно–частотная (амплитудная – АЧХ) представляет собой зависимость отношения амплитуды выходных и входных колебаний от частоты

A(ω)=[Y/X](ω), при 0 ≤ ω ≤∞;

2) фазо – частотная (фазовая – ФЧХ) представляет собой сдвиг по фазе выходных колебаний относительно входных в зависимости от частоты

φ(ω)=φ_вых(ω) - φ_вх(ω);

3) амплитудно - фазовая частотная характеристика (АФЧХ) определяет зависимость от частоты комплексного коэффициента передачи

W(jω) =[Y'/ X'] (ω). (21)

Рассмотрим теперь способы представления различных ЧХ и их связь между собой и другими динамическими характеристиками. АФЧХ W(jω) является комплексной величиной. Если принять комплексную форму записи в соответствии с (19) и (20), то получим

W(jω)= [Y· e ^j(ωt+φ)]/ (X·e^jωt)=(Y/X)·e^jφ.

Если рассматривать изменение ω в определенном диапазоне (обычно 0 ≤ ω ≤∞), то модуль функции W(jω) представляет АЧХ, а ее аргумент -ФЧХ, т.е.

W(jω= A(ω) e^jφ(ω),

A(ω)=I W(jω) I, φ(ω)=arg W(jω).

При использовании алгебраической формы записи комплексного числа W(jω) можно представить в виде суммы вещественной R(ω) и мнимой I(ω) составляющих

W(jω)=R(ω)+j I(ω).

Очевидно, что

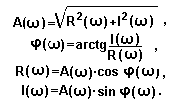
АЧХ и ФЧХ удобно представлять в прямоугольных координатах (рис.19,а,б), АФЧХ -в прямоугольных или полярных. В первом случае по оси абсцисс откладывается вещественная часть, а по оси ординат - мнимая часть АФЧХ (рис.19,в).

В полярной системе координат для каждого фиксированного значения ω длина радиус -вектора равна значению А(ω), а угол между этим вектором и положительной полуосью абсцисс -φ(ω) (рис.19,в).

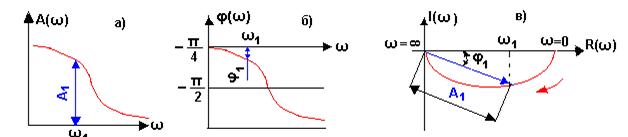
Рис.19 – Графическое представление частотных характеристик

Изображением АФЧХ служит геометрическое место точек концов радиус-вектора (годограф вектора) в положительной плоскости при изменении ω от 0 до +∞. Для частоты- ∞ < ω < 0 получается зеркальное изображение годографа относительно вещественной оси.

Связь между W(jω) и передаточной функцией W(p) устанавливается с помощью интегрального преобразования Фурье F(jω) для периодической функции времени f(t), записываемого в комплексной форме

Преобразования Фурье и Лапласа имеют одну и ту же математическую форму и все операции, относящиеся к прямым и обратным преобразованиям Лапласа, распространяются и на преобразование Фурье. Для нахождения преобразования Фурье для функции f(t) достаточно найти ее преобразование Лапласа и в него вместо оператора р подставить jω:

F[f(t)] = L[f(t)]_p=jω .

Значение для АФЧХ можно получить из W(p) путем подстановки в него вместо р комплексной переменной jω: W(jω)=W(p)_p=jω.

4.3.Логарифмические частотные характеристики

Построение и применение ЧХ (амплитудной и фазовой) значительно упрощается при использовании логарифмического масштаба. Амплитудная ЧХ, построенная в логарифмическом масштабе, называется логарифмической амплитудной частотной характеристикой -ЛАЧХ. При построении ЛАЧХ единицей измерения для оси абсцисс принимается декада, т.е. десятикратное изменение частоты (например, интервал ω от 0,1 до 1) и октаву - двухкратное изменение частоты. Модуль IW(jω)I отсчитывается в логарифмических единицах децибеллах (рис.20). Обозначив ЛАЧХ через L(ω), можно получить ее значение из ординат амплитудно-частотной характеристики А(ω).

Рис.20 –Логарифмический масштаб для ЛАЧХ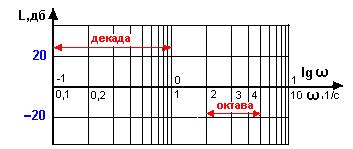

L(ω)=20 lgА(ω), дб.

Децибел является единицей логарифмической относительной величиной. Изменению отношения двух величин в 10 раз соответствует изменение усиления на 20 децибелл. Так как АЧХ А(ω) представляет собой отношение двух амплитуд: амплитуды колебаний на выходе к амплитуде колебаний на входе, то изменению усиления на 20 децибелл соответствует изменению отношения двух амплитуд в 10 раз.

А(ω) 0,0001  0,001  0,01  0,1  1  10  100  1000  10000

L(ω),дб      -80        -60       -40   -20   0  20   40      60       80

Если отношение двух величин рано единице, то усиление равно нулю, т.к. lg 1=0. Это означает, что амплитуды выходных и входных колебаний равны между собой. В случае, когда отношение двух величин меньше единицы, усиление в логарифмическом масштабе будет отрицательным. Отрицательное усиление означает ослабление сигнала или уменьшение амплитуды выходных колебаний по сравнению с амплитудой колебаний на входе. Логарифмическая фазовая частотная характеристика ЛФЧХ строится в полулогарифмическом масштабе - по оси абсцисс откладывается ω в логарифмическом масштабе в декадах, по оси ординат -φ, в угловых градусах или радианах -линейный масштаб. Логарифмические частотные характеристики получили широкое применение в автоматике. Они дают наиболее простой и наглядный способ построения ЧХ, т.к. позволяют аппроксимировать экспериментальные ЧХ, имеющие вид плавной кривой, ломаной кривой, отрезки которой являются асимптотическими прямыми, к которым стремиться ЧХ в данном интервале частот.

Контрольные вопросы

1.Что описывают дифференциальные уравнения САР?
2.Что такое передаточная функция системы регулирования?
3.В чем заключается преобразование Лапласа?
4.Что описывает переходная характеристика?
5.Какие Вы знаете частотные характеристики и что они описывают?
6.В чем смысл преобразования Фурье?
7.Что такое ЛАЧХ?

Вернуться к началу главы

Вернуться к началу учебника