Глава 3.Динамические свойства и характеристики объектов регулирования

3.1.Динамика переходных процессов. Емкость объекта

Динамическими называются свойства объекта регулирования, определяющие особенности переходного процесса, обусловленного возмущением. К ним относятся емкость объекта, самовыравнивание, запаздывание и др. В практике автоматического регулирования под емкостью обычно понимается участок объекта, в котором накапливается вещество или энергия. С этой точки зрения различают одноемкостные, двухемкостные и многоемкостные объекты. Одна емкость всегда связана с другой каким-либо сопротивлением: тепловым, гидравлическим, механическим, электрическим и др. Чем больше величины этих сопротивлений и емкостей, тем медленнее нарастает отклонение регулируемой величины, тем больше время достижения нового установившегося состояния. Емкость объекта характеризуется коэффициентом емкости А. Коэффициент емкости показывает, какое количество вещества или энергии необходимо подвести к объекту или отвести от него, чтобы изменить регулируемую величину, определяющую ход процесса, на единицу измерения. Это определение лучше всего уяснить на простом примере (рис.10). В сосуд с водой поступает некоторое количество воды Q_п (приток), количество воды вытекает Q_с(сток), площадь сечения сосуда F,

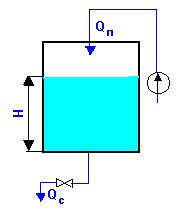
Рис.10 – К коэффициенту емкости

количество воды в сосуде Q. Регулируемой величиной является уровень воды в сосуде Н, который необходимо поддерживать на определенной высоте. Тогда коэффициентом емкости в данном случае будет количество воды, не необходимой для изменения уровня воды в сосуде на 1 м,

А= Q/ Н=( Н∙ F)/ Н= F,

т.е. коэффициент емкости численно равен площади сечения сосуда. При регулировании температуры рабочего пространства печи коэффициент емкости будет равен

A=W/t=(cGt)/t=cG,

где cGt - количество тепла, заключенного в газах, заполняющих печь, в садке и кладке, ограничивающей

              рабочее пространство печи, кДж;

         c - удельная теплоемкость объекта;

         G - масса нагреваемых частей.

Коэффициент емкости может быть постоянным и переменным. В первом примере, если поперечное сечение сосуда не меняется по высоте, то коэффициент емкости будет постоянным. Во втором примере коэффициент емкости будет изменяться в зависимости от температуры, а также от массы нагреваемых частей. В одном объекте можно регулировать не одну, а одновременно несколько величин; например, в нагревательной печи можно одновременно регулировать и температуру и давление. В этом случае коэффициент емкости по температуре будет одной величиной, а по давлению - другой. Коэффициент емкости характеризует скорость изменения регулируемой величины при нарушении равновесия между подачей и потреблением (притоком и стоком). Чем больше при прочих равных условиях коэффициент емкости, тем медленнее будет изменяться регулируемая величина при нарушении нагрузки на объект; чем меньше коэффициент емкости - тем быстрее.

3.2. Самовыравнивание. Статические и астатические объекты

Самовыравнивание - это свойство объекта самостоятельно без участия регулятора при изменении нагрузки возвращаться в установившийся режим работы, но при новом постоянном значении регулируемой величины. Объекты, обладающие самовыравниванием, называются статическими. В таких объектах изменения выходной величины, вызванное возмущением, в свою очередь оказывает обратное действие на приток или сток, направленное в сторону восстановления их равенства. Наличие самовыравнивания в объекте благоприятно сказывается на процессе автоматического регулирования. Обеспечить устойчивое автоматическое регулирование в этом случае обычно оказывается задачей более простой, чем в том случае, если объект вообще не обладает или обладает слишком малой способностью к самовыравниванию. Процесс самовыравнивания легко уяснить на приведенном ранее примере. При увеличении подачи Q_п уровень Н (регулируемая величина) начнет (рис.11) повышаться. Однако, вследствие увеличения гидростатического напора одновременно начнет увеличиваться и количество вытекающей воды Q_с

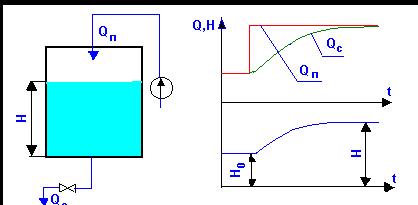
Рис.11- Статический объект. Переходной процесс

и через некоторое время наступит равновесие между притоком и стоком, т.е. Q_п= Q_с, и дальнейшее повышение уровня в сосуде прекратиться. Таким образом, в рассмотренном объекте нарушенное равновесия между притоком и стоком восстанавливается без участия регулятора, но при новом установившемся значении регулируемой величины Н.

Итак, при новом установившемся уровне Q_п= Q_с. Уравнение изменения регулируемой величины ΔΝ в зависимости от изменения расходов ΔQ_п и ΔQ_с получается при совместном решении уравнений:

ΔQ_п - Δ Q_с=F[d(ΔH)/dt] ,

Q_с=f(H,φ),

где φ - перемещение дросселирующего органа в вентиле. При этом предполагается, что сток Q_с линейно зависит от φ линейно Q_с=Кφ где К - коэффициент пропорциональности, зависящий от напора Нρ жидкости над вентилем. При изменении уровня Н и положения задвижки φ в вентиле происходит изменение стока ΔQ_с по уравнению

Δ Q_с=(∂Q_с /∂Н)·ΔН +(∂Q_с /∂φ)·Δφ.

При подстановке значений ΔQ_п и ΔQ_п получим

ΔQ_п- (∂Q_с /∂Н)·ΔН - (∂Q_с /∂φ)·Δφ= F[d(ΔH)/dt] .

Для удобства исследования процессов регулирования приведем последнее уравнение к безразмерному виду. Разделим обе его части на максимально возможный расход Q_max как со стороны стока так и со стороны притока, и отнесем изменение уровня к начальной величине уровня Н₀ :

(ΔQ_п/ Q_max)- (∂Q_с /∂Н)·(ΔН/ Н₀)(Н₀/ Q_max) - (∂Q_с /∂φ)·(Δφ/φ_max)( φ_max/ Q_max)=

=F(Н₀/ Q_max) [d(ΔH/ Н₀ )/dt].

Так как в каждый момент времени Q_с=Кφ, то

(∂Q_с /∂φ)·( φ_max/ Q_max)=1.

Обозначим в последнем уравнении

ΔQ_п/ Q_max=х₁^' - относительное изменение нагрузки со стороны притока;

Δφ/φ_max=х₁^'' - относительное изменение открытия вентиля, приводящее к изменению нагрузки со стороны стока;

ΔH/ Н₀ =х₂ - относительное изменение уровня жидкости в соседе;

(∂Q_с /∂Н)·(Н₀/ Q_max)=К_с - коэффициент пропорциональности, который называется коэффициентом

                        самовыравнивания;

F(Н₀/ Q_max)=Т_с - имеющую размерность времени и называемую постоянной времени объекта.

В результате уравнение приводится к следующему виду

х₁^' - х₁^'' = Т_с(dx₂/dt) + К_сх₂

Это и есть дифференциальное уравнение одноемкостного статического объекта с самовыравниванием, х₁^' - х₁^'' - изменение нагрузки на объект.

Объекты, не обладающие самовыравниванием, называются астатическими. В них изменения выходной величины никакого обратного воздействия на приток и сток не оказывает и при самом малом возмущении выходная величина изменяется непрерывно. Рассмотрим пример. Жидкость подается в сосуд центробежным насосом 1 и откачивается другим насосом 2 (рис.12). В этом случае повышение производительности подающего насоса не отразится на производительности откачивающего насоса.

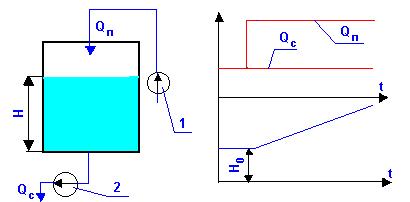
Рис.12 – Астатический объект. Переходной процесс

Уровень жидкости в сосуде будет непрерывно повышаться до тех пор, пока это повышение не нарушит нормальной работы объекта (жидкость перельется через край), или пока внешним вмешательством (вручную или автоматически) не будет изменена производительность насоса 2. Таким образом, данный объект лишен способности к самовыравниванию. Обозначим изменение уровня через ΔH в одноемкостном астатическом объекте. Скорость изменения уровня будет зависеть от разности величин ΔQ_п и Δ Q_с , а также от величины поперечного сечения сосуда F, т.е. коэффициента емкости. Поэтому можно записать

ΔQ_п - Δ Q_с=F[d(ΔH)/dt].

Если предположить, что равновесие нарушилось вследствие изменения одного потока, например, притока, то приведенное уравнение можно переписать следующим образом

F[d(ΔH)/dt]= ΔQ_п ,

из которого после интегрирования получим

ΔH=( ΔQ_п·t)/ F.

Для получения дифференциального уравнения одноемкостного астатического объекта (без самовыравнивания) в общем виде необходимо привести уравнение к безразмерному виду, более удобному для исследования процессов регулирования. Для этого умножим и разделим левую часть уравнения на номинальное значение уровня H_н, а правую часть - на Q_н (номинальное значение притока). Тогда после преобразования получим

[(F· H_н / Q_н) d(ΔH/ H_н]/ dt= ΔQ_п/ Q_н.

Обозначим в приведенном уравнении F· H_н / Q_н =T_a -постоянная времени астатического объекта;

ΔQ_п/ Q_н =х₁ -относительное изменение притока;

ΔH/ H_н =х₂ -относительное изменение уровня.

Тогда уравнение астатического объекта будет иметь вид

T_a·(dx₂/dt)=x₁ .

В уравнениях постоянные времени Т_с и T_a -это промежуток времени, который необходим для того, чтобы при сохранении начальной скорости изменения регулируемой величины последняя достигла бы нового предельного значения. Постоянную времени при изменении нагрузки от нуля до номинального значения часто называют временем разгона объекта, она определяется опытным путем.

В реальном производстве встречаются как статические, так и астатические объекты. Самовыравнивание свойственно, например, всем установкам и агрегатам, являющимися объектами регулирования температуры: плавильным, сушильным и термическим печам, кристаллизаторам и пр. Статическими объектами являются также смесители, глиномешалки, установки для приготовления красок и покрытий и др. Астатическими объектами являются установки, в которых исключено влияние выходной величины на входную, например, кристаллизатор установки непрерывного литья как объект регулирования уровня расплава, поскольку скорость вытяжки слитка не зависит от уровня металла.

3.3. Запаздывание в объектах регулирования

В большинстве объектов регулирования изменение выходной величины начинается не одновременно с возмущением. От момента возмущения до начала изменения выходной величины проходит некоторое время, характеризующее запаздывание в объекте. Различают два вида запаздывания: чистое и емкостное. Чистое запаздывание (передаточное, транспортное, дистанционное) - время, в течение которого выходная величина после возмущения не изменяется. Оно определяется временем, которое необходимо для того, чтобы регулируемая среда прошла от места внесения возмущения до зоны, в которой формируется сигнал о значении выходной величины объекта. Примером элемента с чистым запаздыванием может служить ленточный питатель, с помощью которого осуществляется подача оборотной смеси в бегуны непрерывного действия (рис.13). Оборотная смесь из бункера 1 подается ленточным питателем 2 в

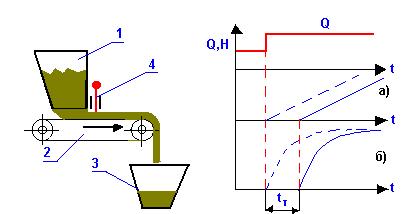
Рис.13 – Объект с чистым (транспортным) запаздыванием

воронку 3 смесителя. Количество материала, поступающего в объект 3 (т.е. приток), зависит от толщины слоя материала на ленте питателя, то есть от положения заслонки 4. При изменении положения заслонки толщина слоя оборотной смеси изменится, однако в объекте 3 приток смеси изменится не одновременно с изменением положения заслонки, а лишь спустя некоторое время t_т, за которое лента питателя переместится от заслонки до объекта. На рис.13 (график) показаны переходные процессы для астатического (а) и статического (б) объектов, причем пунктирные линии для объектов без чистого запаздывания, сплошные линии - при наличии транспортного запаздывания. Такого же характера запаздывание имеет место, например, в домне: изменение количества или теплотворной способности кокса в рабочей колоше лишь тогда скажется на ходе процесса, когда произойдет соответствующее опускание столба шихтовых материалов в шахте печи.

Переходное (емкостное) запаздывание свойственно многоемкостным объектам. Как указывалось ранее, наличие сопротивлений между емкостями объектов вызывает замедление перехода вещества или энергии из одной емкости в другую. Например, в двухемкостном объекте (рис.14) емкости 1 и 2 соединены гидравлическим сопротивлением R .

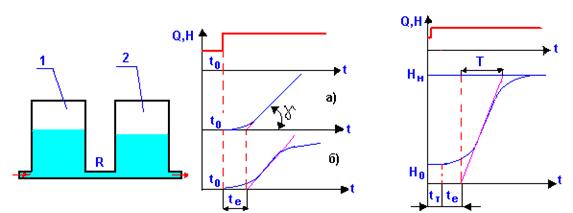
Рис.14 – Объект с переходным запаздыванием Рис.15 – Кривая разгона

Если приток скачкообразно увеличится в момент времени t₀ , то скорость изменения уровня жидкости в емкости 2 будет в течение некоторого времени возрастать от нуля до значения, соответствующего tgγ. На рис.14 (график) показан переходной процесс для объекта без самовыравнивания (а) и с самовыравниванием (б). Время переходного запаздывания определяется отрезком, который отсекает на оси времени касательная к кривой изменения регулируемой величины - t_е . Переходное запаздывание зависит от числа емкостей и величины переходных сопротивлений. При прочих равных условиях емкостное запаздывание более благоприятно, чем чистое запаздывание, так как в случае емкостного запаздывания информация о результатах возмущения поступает на вход регулятора сразу же после возмущения (хотя скорость возмущения и мала), в то время как при транспортном (чистом) запаздывании такой информации нет в течение всего периода запаздывания. В большинстве случаев объектам регулирования свойственно как чистое, так и емкостное. Поэтому при расчетах САР оперируют величиной полного запаздывания:

t_об = t_т + t_е .

Даже для сравнительно простых объектов регулирования не всегда можно точно составить дифференциальное уравнение переходного процесса и тем более рассчитать коэффициенты этого уравнения, прогнозировать величину и характер запаздывания в объекте. Поэтому в тех случаях, когда объект регулирования реально существует (а не проектируется), целесообразно экспериментальное получение его динамических характеристик. Для этих целей наиболее часто используются экспериментальные кривые разгона. Для снятия кривой разгона регулятор (если он был установлен) отключается и в месте установки чувствительного элемента измерительной системы регулятора помещается малоинерционный датчик для регистрации выходной величины объекта. В результате скачкообразного возмущения на входе объекта будет получена кривая разгона, ее характер определяется только динамическими свойствами регулирования. Методика определения этих свойств показана на рис.15. Непосредственно по графику находят постоянную времени объекта Т, потенциальное значение выходной величины, определяется время и характер запаздывания. По этим данным рассчитываются остальные динамические характеристики: коэффициент передачи, коэффициент самовыравнивания, коэффициент емкости, время разгона и др.

Контрольные вопросы

1.Какие характеристики описывают динамические свойства объектов регулирования?
2.Что такое коэффициент емкости объекта регулирования?
3.Дайте определение статическим и астатическим объектам.
4.Приведите дифференциальные уравнения статических и астатических объектов?
5.Какие виды запаздывания характерны для объектов регулирования?
6.Что такое кривая разгона объекта регулирования?

Вернуться к началу главы

Вернуться к началу учебника