Глава 2.Статические характеристики объектов регулирования

2.1.Виды и особенности статических характеристик

Каждому значению входной величины х объекта в установившемся состоянии соответствует определенное значение его выходной величины у. Зависимость между выходной и входной величиной в установившихся состояниях называется статической характеристикой объекта регулирования. Существует два вида статических зависимостей: монотонные и содержащие экстремум. Если статическая характеристика носит монотонный характер (рис.7,а), то для достижения требуемого значения выходной величины необходимо обеспечить однозначно

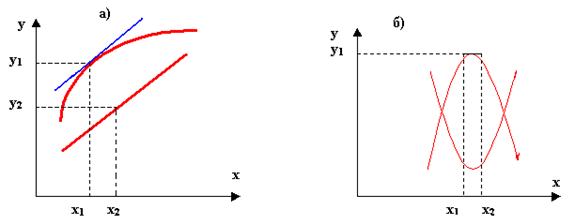
Рис.7 – Статические характеристики объектов регулирования: а) монотонные; б) экстремальные характеристики

определенный уровень входной величины. В экстремальном случае (рис.7,б) такая определенность отсутствует, но возникает другая задача: добиться максимального (или минимального) значения выходной величины, которое достигается при некотором оптимальном уровне входной величины. К числу монотонных статических характеристик относятся, например, такие, как зависимость влажности формовочной смеси от расхода воды, поступающей в бегуны, содержания СО₂ в ваграночных газах от соотношения между расходами дутья и кокса и др. Экстремумы содержаться, например, в статических зависимостях температуры чугуна от коэффициента избытка воздуха; в зависимостях большинства технико-экономических показателей технологических процессов (себестоимость, энергоемкость, производительность и др.) от их входных величин. В случае, если выходная величина является функцией нескольких входных величин, то статическая характеристика изображается на графиках в виде семейства кривых - номограмм.

Аналитически зависимость выходной величины от входной в установившемся режиме принято характеризовать с помощью коэффициента передачи К.

К=dy/dx.

Если статическая характеристика линейна или линеаризована (плавная кривая может быть аппроксимирована прямой линией), то бесконечно малые величины dy, dx могут быть заменены конечными приращениями Δy и Δx .

При расчетах измерительных устройств коэффициент передачи представляется в безразмерной форме:

К=φ/μ,

где φ= Δy/ y₀ – относительное изменение выходной величины;

μ= Δx/ x₀ - относительное изменение входной величины.

Коэффициент передачи не зависит от значения входной величины только в случае, если статическая характеристика средства измерения линейна. Если при изменении входной величины коэффициент передачи изменяется незначительно и этим изменением можно пренебречь, то статическую характеристику можно линеаризовать, например, методом касательной, основанном на известном разложении функции в ряд Тейлора, при этом используется только первый член разложения:

у=у₀+(dy/dx)_х=х0 ·(х – х₀) .

Часто промышленные объекты автоматического регулирования имеют весьма сложные статические зависимости, когда коэффициенты их передачи немонотонно зависят от входной величины в пределах ее рабочего диапазона. В этих случаях линеаризацию удобно выполнять методом усреднения, аппроксимируя исходную зависимость прямой линией так, чтобы отклонение от линеаризуемой кривой было бы наименьшим.

Статическая характеристика, заданная в виде совокупности аналитических зависимостей, таблиц или графиков, представляет собой математическую модель объекта регулирования при функционировании его в установившемся режиме. На основе таких математических моделей разрабатываются и реализуются алгоритмы автоматического управления и регулирования. Математическое описание объекта регулирования может быть получено либо аналитическим, либо экспериментальным методом.

2.2.Аналитические методы получения статических характеристик объектов регулирования

Аналитические методы позволяют получить математическое описание объекта в широком диапазоне изменения его входных и выходных величин. При этом построение модели складывается из следующих этапов:

1) теоретический анализ механизма процессов, происходящих в объекте;

2) выбор процессов, наиболее существенно влияющих на работу объекта;

3) выбор входных и входных величин, характеризующих каждый из рассмотренных процессов;

4) составление и решение систем дифференциальных уравнений переноса и преобразования вещества или энергии в объекте регулирования.

Этот метод получения статических характеристик весьма универсален, но предполагает наличие исчерпывающей информации о механизме процессов, протекающих в объекте регулирования. К сожалению, во многих случаях этот механизм настолько сложен, что его описание дифференциальными уравнениями возможно лишь при идеализации сущности рассматриваемых явлений. Часто подобная идеализация объекта сводит на нет ценность математической модели, так как не обеспечивает получения адекватной статической характеристики. В связи с этим в некоторых случаях отвлекаются от сущности сложных явлений в объекте, рассматривая его лишь как некоторую совокупность входных и выходных величин и находя его статическую характеристику путем анализа и решения уравнений материального или энергетического баланса объекта. При этом математическую модель объекта регулирования получают, используя предпосылку о равенстве прихода и расхода вещества или энергии при стационарном режиме функционирования объекта.

Рассмотрим применение этого метода для определения статической характеристики смесителя непрерывного действия (рис.8). В табл.1 приведены индексы и обозначения характеристик входных и выходных величин.

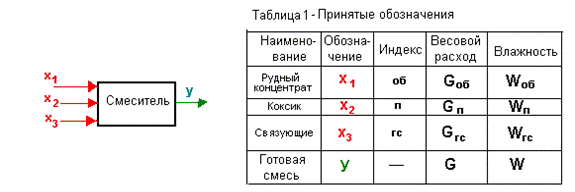
Рис.8 – К расчету статической характеристики смесителя

Уравнение материального баланса смесителя по воде, исходя из равенства ее прихода и расхода в единицу времени:

1/100(G_об W_об +G_пW_п +G_гсW_гс )=[(GW/100)+G_пот],

где G_пот -величина материального баланса, определяемая потерями воды в единицу времени за счет испарения, утечек и т.д. Из уравнения следует, что статическая характеристика имеет вид:

W=( G_об W_об +G_пW_п +G_гсW_гс - 100G_пот)/G.

Дифференцируя уравнение (3) по соответствующим аргументам, получим коэффициенты передачи:

K₁=∂W/∂G_об=(W_об)₀/G₀ ; K₂=∂W/∂W_об=(G_об)₀ /G₀ ; K₃=∂W/∂W_гс=(G_гс)₀ /G₀ и т.д.

Как следует из изложенного, данный метод получения статических характеристик прост в расчетном отношении, но требует учета всех статей прихода и расхода вещества или энергии. Если величина G_пот при этом оказывается пренебрежимо малой или поддается прогнозированию, то статическая характеристика адекватна, в противном случае будут получены неудовлетворительные результаты.

2.3.Экспериментальный метод построения статических характеристик

В тех случаях, когда нельзя воспользоваться аналитическими методами, статические характеристики получают на основании экспериментальных данных. При активном эксперименте производят целенаправленное изменение входных величин объекта регулирования и фиксируют реакцию объекта на эти искусственные возмущения после достижения нового установившегося состояния. Пассивный эксперимент заключается лишь в наблюдении за состоянием объекта с фиксацией произвольно изменяющихся значений входных и выходных величин при различных равновесных режимах.

В табл.2 приведены в качестве примера результаты экспериментального изучения зависимости температуры жидкого чугуна t,^o C (выходная величина) от удельного расхода Q дутья на м² площади сечения доменной печи при расходе кокса около 15%.

Таблица 2-Результаты эксперимента

№ п/п	1	2	3	4	5	6	7	8	9	10
Q	170	120	120	190	190	150	130	140	150	150
t,^oC	1380	1320	1300	1390	1400	1360	1310	1330	1340	1360

 Из таблицы видно, что при переходе от опыта к опыту входная величина Q изменялась некоторым беспорядочным образом. Такое не упорядочное изменение имеет ряд преимуществ перед монотонным варьированием входной величины. Действительно, во время плавки изменяются размеры и количество кокса и других шихтовых материалов, температура и влажность воздуха, высота холостой и рабочей колоши, сечение шахты и др. Некоторые из этих факторов изменяются во времени незакономерным образом, в то время как другие (например, сечение шахты) имеют плавный характер изменения. На рис.9 показана экспериментальная линия регрессии (кривая 1) и расчетная линия регрессии 2.

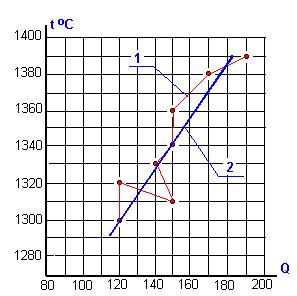
Рис.9 – Экспериментальная статическая характеристика

При линейной аппроксимации статической характеристики расчетное уравнение регрессии имеет вид:

t=a₀ +a₁Q,

где a₀ и a₁ - коэффициенты регрессии.

При статистической обработке экспериментальных данных коэффициенты в уравнении регрессии определяются методом наименьших квадратов, обеспечивающего минимум суммы квадратов отклонений экспериментальных точек от расчетных значений. Метод наименьших квадратов может быть использован и для получения линеаризованной многофакторной статической характеристики объекта регулирования. Найденные по методу наименьших квадратов коэффициенты регрессии фактически являются коэффициентами передачи изучаемого объекта.

Контрольные вопросы

1.Назовите виды статических характеристик объектов регулирования.
2.Что такое коэффициент передачи объекта регулирования?
3.В чем заключается аналитический метод построения статических характеристик?
4.Объясните экспериментальный метод построения статических характеристик.

Вернуться к началу главы

Вернуться к началу учебника